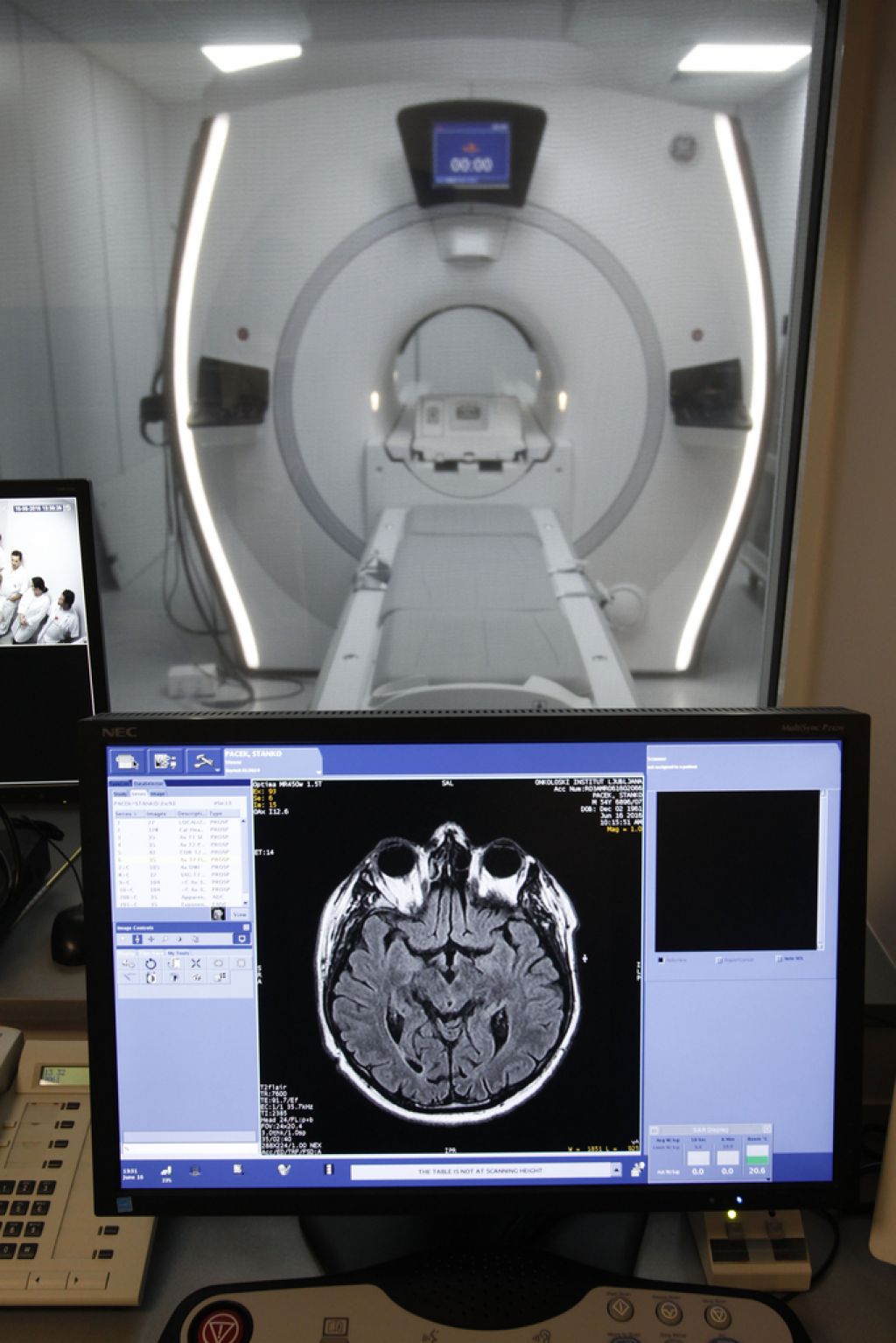
Slikanje z magnetno resonanco omogoča odličen globinski pogled v mehka tkiva. Metoda je nenevarna, a draga. Toda nove tehnike vzorčenja obljubljajo izboljšano sliko in hitrejši zajem, kar je zelo pomembno pri diagnostiki.
Matematikom se je v zadnjih dveh desetletjih posrečilo razviti in teoretično utemeljiti novo metodo strnjenega vzorčenja (snemanja, zajemanja), ki ji v angleščini pravijo compressed sensing, compressive sampling. Ta omogoča, da v določenih okoliščinah in kadar nas zanima le majhno število podatkov, dobimo dobro sliko stanja z bistveno manj meritvami, kot smo bili navajeni.
Za razumevanje magnetne resonance in strnjenega vzorčenja si lahko pomagamo z metodami, ki jih uporabljamo pri zajemanju in shranjevanju zvočnega signala.
Zvočni signal lahko digitaliziramo, tako da zapišemo njegove trenutne vrednosti (vzorce) v kratkih časovnih presledkih. Temu pravimo vzorčenje. Znameniti Shannonov izrek iz leta 1948 pravi: signal, ki vsebuje le frekvence pod n, moramo vzorčiti vsaj s frekvenco 2n, torej vsaj 2n-krat na sekundo. Potem lahko iz vzorcev natančno rekonstruiramo original (podobne rezultate so že pred Claudom Elwoodom Shannonom dokazali nekateri drugi matematiki, denimo Vladimir Kotelnikov leta 1933).
Ljudje navadno ne slišimo zvokov nad 20 kilohercev. Torej moramo za dobro digitalizacijo glasbe najprej »odfiltrirati« vse zvoke s frekvenco nad 20 kHz in nato vzorčiti s frekvenco več kot 40 kHz. Za kakovost zapisa, kakršnega uporabljamo na glasbenih ploščah cd, vzorčimo s frekvenco 44,1 kHz. To nam omogoča, da iz vzorcev zvesto rekonstruiramo (sfiltrirani) original. Pri digitalni telefoniji vzorčimo le z 8 kHz, kajti telefoni so zasnovani za frekvenčno območje od 300 Hz do 3,4 kHz. To je bolj zasilna rešitev, saj človeški glas sega nekako od 60 Hz do 14 kHz. Gostejše vzorčenje in boljšo kakovost zvoka že zdaj ponuja Skype. Uvajajo tudi nove rešitve kot HD voice (vzorčenje s 16 kHz). Gostejše vzorčenje seveda pomeni večjo količino podatkov in večje obremenitve pri prenosu (vse povedano velja, ustrezno prilagojeno, tudi za digitalizacijo fotografij).
Aliasing ali napaka
Rekonstrukcija signala nam lahko da povsem napačen rezultat. Take učinke v fotografiji in pri videu navadno označimo s francosko besedo moiré. Zaradi aliasinga (interakcije med fino strukturo na tekstilu in za to strukturo preveč redkim razporedom pikslov na senzorju kamere, se pravi premalo gostim vzorčenjem) bodo pri rahlih premikih osebe na posnetku nastala čudna valovanja na tekstilu. Zato na televizijski intervju ni pametno priti z obleko z gostim črtastim ali karirastim vzorcem.
Kaj pa, če bi vzorčili na redko, ampak ne v enakomernih presledkih, temveč v naključno izbranih točkah? V tem primeru je manj verjetno, da pridemo do napačnih rezultatov.
Vzorčenje z naključnim korakom je ena od idej za strnjeno vzorčenje. Začetek tega pristopa sega v sedemdeseta leta prejšnjega stoletja. Geologi, ki so iskali nafto, so eksperimentalno ugotovili, da lahko dobijo želeno sliko zemeljskih slojev z mnogo manj seizmičnimi meritvami, kot bi jih bilo potrebnih po teoriji.
Geologija človeškega telesa
To je bila seveda odlična novica, saj je povzročanje mini potresov z eksplozivom ali odmetavanjem težkih bremen s helikopterja drago in moteče. Zadevo so si razložili s tem, da so posamezni sloji precej homogeni. Zanimale so jih le meje med sloji, ki so na instrumentih dajale špice, in pa prisotnost sloja, ki bi lahko vseboval nafto. Skratka, zanimalo jih je le majhno število pomembnih informacij. V devetdesetih letih so metode geologov začeli proučevati matematiki, med njimi David Donoho z univerze Stanford.
Bi bilo mogoče podoben pristop uporabiti tudi za ugotavljanje »geologije« človeškega tkiva? Vsekakor, saj slikanje z magnetno resonanco (magnetic resonance imaging ali MRI) omogoča prav to: odličen globinski pogled v mehka tkiva. Za to metodo sta kemik Paul Lauterbour in nedavno umrli sir Peter Mansfield leta 2003 prejela Nobelovo nagrado za fiziologijo in medicino. Pri razvoju MRI pa so uspešno sodelovali naši fiziki. Profesor Ivan Zupančič je konstruiral tuljave, potrebne za prvo različico naprave. Skupina profesorja Janeza Stepišnika ima dolg staž v raziskavah na področju MRI. Profesor Gorazd Planinšič je več let sodeloval v skupini profesorja Mansfielda, podobno krajši čas dr. Miha Kos.
Francoski matematik Emmanuel Candès s Caltecha in njegov mentor pri doktoratu David Donoho sta oba začela ugotavljati, da lahko dobita dobre slike vzorcev MRI tudi s precej manj posnetki, kot jih predvideva Shannonova teorija, če vzorčita nekoliko drugače. Tako kot pri običajnih fotografijah tudi pri MRI navadno ni vse na sliki zanimivo.
Digitalno sliko ali zvok lahko skoraj zmeraj močno stisnemo (slike denimo v format jpeg, zvok v mp3) z minimalno izgubo kakovosti. Vendar je treba najprej zajeti čisto vse podatke, da se potem odločimo, katere tri četrtine (ali še večji delež) lahko odvržemo. Izjema so slike z ogromno podrobnostmi, ki jih ne moremo kaj dosti stisniti, ne da bi izgubili podrobnosti.
Pri strnjenem vzorčenju je postopek drugačen: že vnaprej želimo zajeti manj podatkov, kot jih zahteva Shannonov pogoj, in se obenem izogniti napakam. Toda takšna metoda je učinkovita samo takrat, kadar iščemo majhno število informacij.
Kakovostno stiskanje
Kaj to pomeni v praksi? Spomnimo se na tale problem: imamo devet kovancev, med katerimi jih ima osem enako maso, eden pa je lažji. Le z dvema tehtanjema s staromodno ravnovesno tehtnico, brez uteži, lahko najdemo lažji kovanec, če se tega lotimo pravilno.
Candès je imel na konferencah ob predstavitvi svojih rezultatov težave, ker so nekateri mislili, da malce goljufa. Poskušal je stvari strogo dokazati, a se mu je po prvih uspehih zataknilo. Naključje je hotelo, da je imel Candès otroka v isti mali šoli kot Terence Tao z UCLA. (Tao je nekaj let kasneje dobil Fieldsovo medaljo, eno najprestižnejših nagrad v matematiki.) Francoz je Tau zaupal svoje probleme, a mu sogovornik najprej ni verjel in mu je obljubil protiprimer za njegove trditve. Protiprimera pa ni mogel najti, zato je stvar vzel resneje, začel sodelovati s Candèsom in prispeval manjkajoči dokaz. Z njima je delal Justin Romberg z Georgia Tech. Preprint njihovih rezultatov je izšel leta 2004, obenem pa je Donoho oznanil podobna dognanja. V njihovi teoriji gre za rekonstrukcijo signalov: vektorjev ogromne dolžine (razsežnosti), denimo reda velikosti milijon ali več. Vemo pa še, da ima signal zelo malo koordinat, različnih od nič. Signal želimo rekonstruirati iz meritev, ki so na znan način linearno odvisne od signala. Običajno bi potrebovali toliko meritev, kot je dolžina signala. Candès, Romberg in Tao so leta 2006 v reviji IEEE Transactions on Information Theory objavili članek, v katerem so dokazali, da pri določenih pogojih z verjetnostjo blizu 1 rešitev dobimo iz bistveno manjšega števila meritev.
Rezultati so torej tesno povezani z verjetnostjo. Pri iskanju rešitve uporabimo že dolgo znane metode linearnega programiranja. Morda se bo kdo hudoval, da točnost rekonstrukcije ni gotova, ampak le zelo zelo verjetna. Ampak v praksi tudi klasično gosto vzorčenje zaradi pomanjkljivosti algoritmov za rekonstrukcijo včasih privede do napak.
Sekunde namesto minut
Teorija je zelo zanimiva, a do nedavnega sta obstajala dva problema. Pri mnogo zamišljenih aplikacijah ni bilo čisto jasno, kako inženirsko sprejemljivo izvesti meritve. Drugi problem pa je bila računska zahtevnost metode. No, konec lanskega novembra je Siemensovo podjetje napovedalo, da začenjajo prodajati opremo za slikanje z magnetno resonanco, ki sloni na strnjenem vzorčenju. Namenjena je slikanju delovanja srca. Po njihovih napovedih lahko naprava v 25 sekundah naredi tisto, za kar so potrebovali prej do šest minut. Pacient mora samo enkrat zadrževati dih namesto desetkrat do štirinajstkrat, kot pri prejšnjem postopku. Obdelava podatkov poteka v sami napravi.
Skrčitev morda ne gre samo na račun strnjenega vzorčenja, ampak tudi drugih algoritemskih in inženirskih izboljšav. Vseeno je to zmagoslavje tako teoretične kot uporabne matematike. Namesto več meritev lahko uporabimo več pameti. Hkrati je to še en dokaz, da lahko tudi vrhunski raziskovalci na abstraktnem področju teoretične matematike kot Terence Tao prispevajo k tehničnemu napredku.
Prve različice te inovacije so v uporabi že vsaj leto dni v uglednih bolnišnicah. Pri Siemensu obljubljajo, da bodo kmalu ponudili podobne naprave tudi v druge namene. Videli bomo, kdaj bodo sledili drugi ponudniki tovrstne opreme.
Strnjeno vzorčenje bi lahko bilo uporabno marsikje, kjer so tipala zelo draga. Verjetno se bo pojavilo tudi pri računalniški tomografiji (CT) in zmanjšalo hude doze ionizirajočega sevanja, ki smo jim izpostavljeni pri tej rentgenski diagnostiki.
prof. dr. Peter Legiša, Fakulteta za matematiko in fiziko Univerze v Ljubljani
 Tiskane izdaje
Tiskane izdaje